Division fractale
pseudo-aléatoire
des triangles isogonoïdes
|
Un triangle est dit isogonoïde si tous ses angles sont supérieurs à pi/6 (30 degrés). On ne va pas le démontrer ici, mais il est toujours possible de découper un triangle isogonoïde en... pas mal de triangles tous isogonoïdes. Ici, on va se fixer pour règle de toujours le diviser en un nombre pair de triangles isogonoïdes, de façon que tous ces sous-triangles, même ceux des bords, soient censés avoir un triangle voisin et un seul sur chacun de leurs trois côtés. Cela force à établir des relations purement logiques (non géométriques) pour les sous-triangles du pourtour ; c'est sans doute un peu abstrait, mais ce n'est pas difficile. Ensuite de quoi, on va colorier ces sous-triangles avec deux couleurs, en se fixant pour règle que chaque sous-triangle soit toujours de la même couleur que la majorité de ses trois voisins. On obtient donc une figure du type de celle qui suit :  Ensuite, on va appliquer la même logique sur chacun des sous-triangles, en imposant en plus que la couleur majoritaire sur ses sous-sous-triangles soit celle qu'il portait avant cette subdivision. 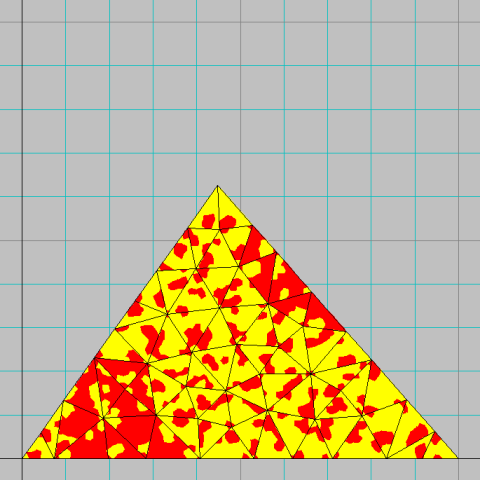 Voilà ce que ça donne au bout de seulement deux générations. On voit que cela fait apparaître des formes complexes, non dénuées de rapport avec la première génération, mais quand même déjà assez différentes visuellement. 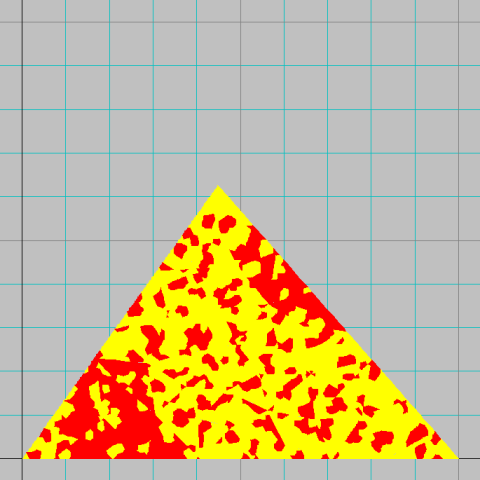 Rien n'empêche en théorie de recommencer le processus pendant un nombre quelconque de générations, ce qui mène à la constitution de formes infiniment complexes. |